Updated 2015-01-01 19:13:24 by dkf ▲

Richard Suchenwirth 2004-05-02 -- In this weekend fun project I played with simulation of digital hardware, namely "full-adders". While these are not spectacular in effect (they just put 1 and 1 together), they are essential for integer additions. In a 32-bit machine, you'd have 32 of such full-adders in parallel, but in this plaything I limited the "word-width" to three, as the principle should be clearer so. At least you can use it for additions up to 7+7=14...

A full-adder has three input lines: the two "bits" to add, and a carry from the previous full-adder (drawn at right); and two outputs, namely the one-bit result of the addition, and its own carry. The following plaything contains

  • three adders, named a, b, and c, which are wired to
  • input switches (checkboxes) which you can turn on or off, and
  • "lamps" (the round things on the bottom), which turn bright or dark depending on whether they get "power".

To make things even more pedagogical, the wires also change color to red when they carry power. When a checkbox is clicked, communication between the components goes via traces: the checkbox notifies its wire, which changes color accordingly and sets the variable at the end of the wire. When an input to a full-adder changes, its outputs are recomputed, triggering the out wires, which again change color and update their other end. Testing made me think it all works as it should.

Innocent as they look here, full-adders are in fact built up from two half-adders (two lines in, two lines out) and an OR gate, while half-adders themselves can be built up from five NAND gates ("a" above needs only be a half-adder, as no carry can come to him). A NAND gate, finally, can be implemented from two transistors. So to build this plaything in real discrete hardware, you'd have to wire the equivalent of 53 transistors together... My patience would fail long before that - good that we can simulate wiring in Tcl :)
proc main argv {
    set w [canvas .c -width 160 -height 160]
    pack $w
    foreach x {40 80 120} name {p3 p2 p1} {input $name $w $x 20}
    foreach x {60 100 140} name {q3 q2 q1} {input $name $w $x 50}
    adder a $w 130 80
    adder b $w 90  100
    adder c $w 50  120
    foreach x {20 60 100 140} name {r4 r3 r2 r1} {
       lamp $name $w $x 150
    }
    #-- wires from inputs to adders:
    wire $w p1 a1
    wire $w q1 a2
    wire $w p2 b1
    wire $w q2 b2
    wire $w p3 c1
    wire $w q3 c2
    #-- carry lines between adders:
    wire $w a4 b3
    wire $w b4 c3
    #-- to lamps:
    wire $w a5 r1
    wire $w b5 r2
    wire $w c5 r3
    wire $w c4 r4
}
# Hardware components:
proc input {name w x y} {
    checkbutton $w.$name -variable $name -onvalue 1 -offvalue 0
    $w create window $x $y -window $w.$name
    set ::g($name) [list $x $y]
}
proc adder {name w x y} {
    global g ${name}1 ${name}2 ${name}3 ${name}4 ${name}5 
    $w create rect [- $x 12] [- $y 7] [+ $x 12] [+ $y 7]
    $w create text $x $y -text $name
    set g(${name}1) [list [- $x 10] [- $y 7]]
    set g(${name}2) [list [+ $x 10] [- $y 7]]
    set g(${name}3) [list [+ $x 12] $y]
    set g(${name}4) [list [- $x 10] [+ $y 7]]
    set g(${name}5) [list [+ $x 10] [+ $y 7]]
    foreach i {1 2 3 4 5} {set ::$name$i 0}
    foreach i {1 2 3} {trace var $name$i w "add $w $name;#"}
}
proc add {w name} {
    global ${name}1 ${name}2 ${name}3 ${name}4 ${name}5 
    set sum [expr [set ${name}1]+[set ${name}2]+[set ${name}3]]
    set ${name}4 [expr $sum>1] ;# carry
    set ${name}5 [expr $sum%2] ;# lsb
}
proc lamp {name w x y} {
    global $name
    $w create oval [- $x 6] [- $y 6] [+ $x 6] [+ $y 6] -fill black -tag $name
    set ::g($name) [list $x $y]
    set $name 0
    trace var $name w "toggleLamp $w $name ;#"
}
proc toggleLamp {w name} {
    global $name
    $w itemconfig $name -fill [expr {[set $name]? "yellow": "black"}]
}
proc wire {w from to} {
    global g
    foreach {x0 y0} $g($from) {x1 y1} $g($to) break
    set ym [expr ($y0+$y1)/2]
    $w create line $x0 $y0 $x0 $ym $x1 $ym $x1 $y1 -tag $from
    trace var ::$from w "toggleWire $w $from $to;#"
}
proc toggleWire {w from to} {
    global $from $to
    $w itemconfig $from -fill [expr {[set $from]? "red" : "black"}]
    set $to [set $from]
}
# Shortcut math:
foreach op {+ -} {proc $op {a b} "expr \$a $op \$b"}
 
main $argv
bind . <Escape> {exec wish $argv0 &; exit}

For a more intuitive picture of a full adder, see http://micro.magnet.fsu.edu/creatures/pages/fulladder.html :)

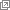See also: Nicholas Pippenger: Complexity of Addition available in MPEG format here: [1]

The behavior of a full-adder can be implemented by currying a generic proc as follows: lgate takes a list of output "lines" which indicate the 0/1 result for a given combination of the inputs, which form the rest of the arguments.
proc lgate {outputs args} { 
   set res {} 
   foreach pattern $outputs { 
       set index 0 
       set fac 1 
       foreach arg $args { 
          if $arg {incr index $fac} 
          incr fac $fac ;# double it 
       } 
       lappend res [string index $pattern $index] 
   } 
   set res 
}

First, try a half-adder:
 % lgate {0110 0001} 0 0 
 0 0 
 % lgate {0110 0001} 0 1 
 1 0 
 % lgate {0110 0001} 1 0 
 1 0 
 % lgate {0110 0001} 1 1 
 0 1

Works as specified. Now for the full-adder:
 % lgate {01101001 00010111} 0 0 0 
 0 0 
 % lgate {01101001 00010111} 0 0 1 
 1 0 
 % lgate {01101001 00010111} 0 1 1 
 0 1 
 % lgate {01101001 00010111} 1 1 1 
 1 1

So we can implement the pure workings of the full-adder (still missing: assignment to output variables) as follows:
interp alias {} full-adder {} lgate {01101001 00010111}

or any other combination of m inputs and n outputs, just defined by n strings of 2**m bits... Explained: given this truth table for the half-adder, a, b and c are the inputs, and p and q its outputs, and each row is a case:
 c b a   p q
 0 0 0   0 0
 0 0 1   0 1
 0 1 0   0 1
 0 1 1   1 0
 1 0 0   0 1
 1 0 1   1 0
 1 1 0   1 0
 1 1 1   1 1

The input part is just an enumeration of possible states (counting up binary numbers); so each column of the output part is already a full specification of the behavior of that output under all circumstances.

TV (May 12 '04) I'll take a remark from RS on the tcl chat serious, and at least add a pointer to a related BWise page: simulating latch behaviour in Bwise where the bits of a graphical block input and output pins are shown as 0 or 1 instead of ticks. Maybe I should make the above into a bwise block. Almost starts to look like computer structures then: register blocks and adders....

See also Playing with circuits where I have unwittingly reinvented parts of the above code. I really have to do more research (at least in my own works) before starting a new fun project... - RS

Arts and crafts of Tcl-Tk programming[Category Electronics]